다익스트라 알고리즘 (Dijkstra Algorithm)
다익스트라 알고리즘은 한 정점에서 모든 정점까지의 최단 거리를 각각 구하는 알고리즘이다.
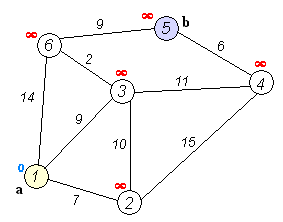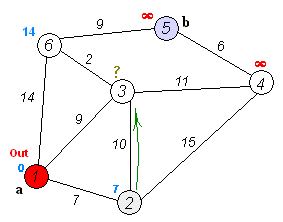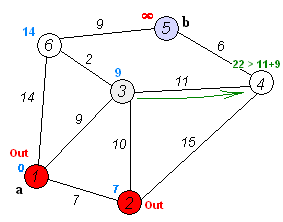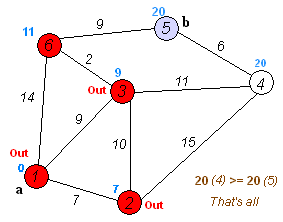
다익스트라 알고리즘 탐색 과정
[step 1] 출발 노드와 도착 노드를 설정
[step 2] 출발 노드를 기준으로 각 노드의 최소 비용을 저장 ( 갈 수 없다면 INF로 설정)
[step 3] 방문하지 않은 노드 중에서 비용이 가장 적은 노드를 선택
[step 4] 해당 노드를 거쳐서 특정 노드로 가는 경우를 고려하여 최소 비용 갱신
[step 5] 3,4 과정을 반복
다익스트라 알고리즘 탐색 예시
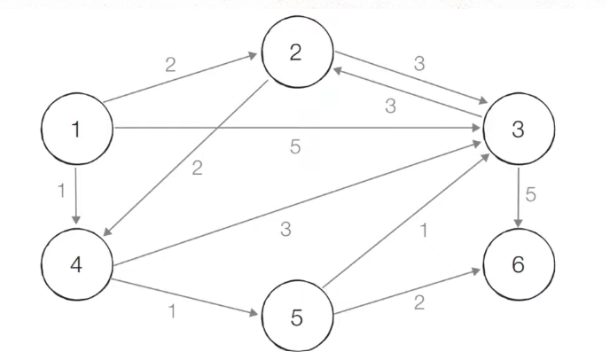
이차원 배열 형태로 그래프를 처리
| 출발/도착 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 0 | 2 | 5 | 1 | INF | INF |
| 2 | INF | 0 | 3 | 2 | INF | INF |
| 3 | INF | 3 | 0 | INF | INF | 5 |
| 4 | INF | INF | 3 | 0 | 1 | INF |
| 5 | INF | INF | 1 | INF | 0 | 2 |
| 6 | INF | INF | INF | INF | INF | 0 |
출발 노드를 1, 도착 노드를 6으로 설정하고 최소 비용 테이블을 초기화
| 0 | 2 | 5 | 1 | INF | INF |

현재 방문하지 않은 노드 중 비용이 최소인 4번 노드 선택
4번 노드를 거쳐서 갈 수 있는 경우를 고려하여 최소 비용 배열을 갱신
| 0 | 2 | min(5, 1+3) = 4 | 1 | min(INF, 1+1) = 2 | INF |

방문하지 않은 노드중 비용이 최소인 2번 노드 선택( 비용이 같을 경우 작은 인덱스 선택)
2번 노드를 거쳐 갈 수 있는 경우를 고려하여 최소 비용 배열 갱신
| 0 | 2 | 4 | 1 | 2 | INF |

방문하지 않은 노드중 비용이 최소인 5번 노드 선택
5번 노드를 거쳐갈 수 있는 경우를 고려하여 최소 비용 배열 갱신
| 0 | 2 | min(4, 2+1) = 3 | 1 | 2 | min(INF, 2+2) = 4 |

방문하지 않은 노드 중 비용이 최소인 3번 노드 선택
3번 노드를 거쳐갈 수 있는 경우를 고려하여 최소 비용 배열 갱신
| 0 | 2 | 3 | 1 | 2 | min(4, 3+5) = 4 |
최종적으로 1번에서 6번까지 가는데 1 - 4 - 5 - 6 경로를 거치고, 최소 거리는 4이다.
다익스트라 알고리즘 코드 - 1
import sys
INF = (1e9)
n = int(input()) # 노드의 갯수 n
m = int(input()) # 간선의 갯수 m
start = int(input())
# 그래프 초기화
graph = [[] for i in range(n + 1)]
# 방문 여부를 기록
visited = [False]*(n+1)
# 최단 거리 기록
distance = [INF] * (n+1)
for _ in range(m):
#a에서 b로 가는 비용 c
a,b,c = map(int,sys.stdin.readline().rstrip().split())
graph[a].append((b,c))
# cost가 최소인 노드 찾기
def get_smallest():
min_value = INF
index = 0
for i in range(1,n+1):
if distance[i] < min_value and not visited[i]:
min_value = distance[i]
index = i
return index
def dijkstra(start):
# 시작 노드의 거리를 0으로 설정 및 방문 처리
distance[start] = 0
visited[start] = True
# 시작노드와 연결된 노드의 거리 설정
for j in graph[start]:
distance[j[0]] = j[1]
for _ in range(n-1):
# 현재 cost가 최소인 노드
now = get_smallest()
# 방문 처리
visited[now] = True
# 현재 방문중인 노드에 대해 거리 갱신
for j in graph[now]:
cost = distance[now] + j[1]
if cost < distance[j[0]]:
distance[j[0]] = cost
dijkstra(start)
for i in range(1,n+1):
print(-1 if distance[i] == INF else distance[i], end = " ")다익스트라 1의 시간 복잡도
- get_smallest()
- 반복문을 통해 방문하지 않은 노드중 cost가 최소인 노드를 찾는다. 이 함수는 다익스트라 함수에서 n-1 번 반복되므로 시간 복잡도는 O(n^2)이다.
- dijkstra()
- 모든 노드에 대해 초기 거리를 설정하는 시간 복잡도는 O(m)
- 다익스트라 알고리즘의 전체 시간복잡도는 O(n^2 + m) 이므로 최종적인 시간 복잡도는 O(n^2)이다.
다익스트라 알고리즘 코드 - 2 ( 우선순위 큐 사용)
두번째 방법은 heap 자료구조를 사용한다.
2024.08.07 - [📖코딩테스트/Python] - [Python] heapq 라이브러리
[Python] heapq 라이브러리
힙큐(heapq)는 파이썬 표준라이브러리가 제공하는 모듈로 Heap 자료구조를 지원한다. 완전 이진트리 형태를 하고 있으며, 최솟값과 최댓값을 빠르게 찾을 수 있다 . 파이썬은 기본적으로 최소힙(m
yobi-devlog.tistory.com
import sys
import heapq
INF = int(1e9)
n = int(input()) # 노드의 갯수 n
m = int(input()) # 간선의 갯수 m
start = int(input()) # 시작 지점
graph = [[] for _ in range(n+1)]
distance = [INF] * (n+1)
for _ in range(m):
# a에서 b로 가는 비용 c
a,b,c = map(int,sys.stdin.readline().rstrip().split())
graph[a].append((b,c))
def dijkstra(start):
queue = []
# 힙에 시작 위치를 삽입
heapq.heappush(queue, (0, start))
distance[start] = 0
# 큐에 노드가 있는 동안 실행
while queue:
# 힙에서 cost가 최소인 노드 pop
dist, now = heapq.heappop(queue)
# 해당 노드의 cost가 distance에 기록된 값보다 크다면 패스
if distance[now] < dist:
continue
# distance 갱신
for i in graph[now]:
cost = dist + i[1]
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(queue, (cost, i[0]))
dijkstra(start)
for i in range(1, n+1):
print(-1 if distance[i] == INF else distance[i], end = " ")다익스트라 2의 시간 복잡도
- 우선순위 큐를 사용하여 최단 경로를 가진 노드를 선택한다.
- 우선순위 큐에서 원소를 삽입하거나 제거하는 데 걸리는 시간은 O(log n) 이다.
- 다익스트라 메인 루프에서 큐에 노드가 있는 동안 각 노드에 대해 인접한 모든 노드를 탐색한다.
- 각 간선을 따라 최단 거리를 계산하고 새로운 최단 거리가 발생할 때 마다 큐에 삽입한다.
- 모든 간선에 대해 이루어지므로 간선의 수 m에 비례한 시간이 소요된다.
- 최종적인 시간 복잡도는 O(m log n)이 소요된다.
다익스트라 알고리즘의 장단점
- 장점
- 단일 시작점에서 모든 노드로의 최단 경로 탐색 가능
- 우선순위 큐를 사용하면 효율적인 탐색 가능
- 단점
- 음수 가중치가 있는 그래프에서는 사용 불가능 (벨만-포드 알고리즘 사용 대안)
- 모든 경로를 탐색하지 않는다. (복수의 경로 제공 x)
함께 보면 좋은 문제
1753. 최단 경로
'🤔알고리즘' 카테고리의 다른 글
| [알고리즘] 크루스칼 알고리즘 (Kruskal Algorithm) (0) | 2024.08.29 |
|---|---|
| [알고리즘] BFS (너비 우선 탐색) (0) | 2024.08.20 |
| [알고리즘] DFS (깊이 우선 탐색) (0) | 2024.08.20 |
| [알고리즘] 백트랙킹 (Backtracking) (0) | 2024.08.20 |
| [알고리즘] 플로이드 워셜 알고리즘 (Floyd - Warshall Algorithm) (0) | 2024.08.17 |